東京大学 特別教授/名誉教授
東京大学国際高等研究所
ニューロインテリジェンス国際研究機構副機構長
合原 一幸先生

【ご講演内容】
研究やビジネスの最前線を走る“現代の偉人”を講師に迎える「トップリーダーと学ぶワークショップ」。今回は東京大学国際高等研究所の合原一幸先生をお招きして「数学をいかにして社会のために役立てるか?」をテーマに、社会と密接に結びつく数学や、最先端の数理工学が導く未来の社会について講演いただいた。
高校生の皆さんにとって数学の研究といえば、素数のパターン追求やフェルマーの定理の証明などを思い浮かべるでしょう。これらのいわゆる純粋数学に対して、私たちが取り組むのは数理工学です。数理に工学がつく理由は、興味の対象が世の中に向けられていて、実世界の問題解決のための方法論として数学を使うからです。
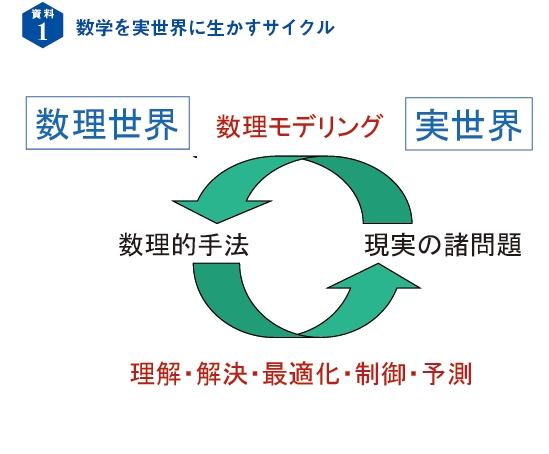
現実の諸問題を数学的に研究するためには、まず問題を数学の世界に取り込む必要があります。数学を言語として現実を表現するプロセスが「数理モデリング」です。これにより「数理モデル」ができると、現実の問題を数学的に理解し、その解決から最適化や制御、予測へと導いていけるのです(資料1)。
数理工学のなかでも私は、主に「複雑系」と呼ばれる分野に取り組んできました。21世紀に残された多くの問題、例えば脳や病気、感染症などから環境、エネルギー、通信、情報そして経済など重要課題の多くは、複雑系の問題として捉えられます。
複雑系の典型例が脳です。脳では1000億個の神経細胞からなるネットワークが相互作用し、その結果として意識が生まれます。そして、その生まれた意識から影響を受けて神経細胞の活動が変わり、相互作用も変わっていく。つまり全体と部分が常に循環している。この循環が複雑系を捉えるときの難しさであり、かつ、おもしろい点でもあります。
複雑系を理解するためのプラットフォームを三つの理論によって構築しました。複雑系のダイナミクスを対象とする「複雑系制御理論」、要素間の関係性やネットワーク構造を解析する「複雑ネットワーク理論」、ビッグデータを解析するための「非線形データ解析理論」です。この理論的プラットフォームを使ってさまざまな複雑系を調べています。
そして数学の考え方は、論理的にものごとを考えるための基盤なので、文系理系問わずに身につけたい考え方です。
資料1
複雑系の次に覚えてほしい用語が「非線形」です。高校レベルで学ぶさまざまな法則は、基本的に「線形」です。例えばオームの法則V=RI(V:電圧、I:電流、R:電気抵抗)などの特性は直線で表せるので「線形特性」と呼びます。
ところが実際の世の中の現象では、特性が必ず曲がります。曲がる、すなわち線形ではないので「非線形」と呼びます。その典型例が二次関数です。だから二次関数を理解できれば、世の中のいろいろな非線形現象を理解できるようになります。
例えば二次関数y=ax(1-x)を考えましょう。ここで、aはパラメーターです。この二次関数のxを時刻tの値x(t)、yをその次の時刻t+1の値x(t+1)と読み替えます。するとx(t+1)=ax(t)(1-x(t))という非線形の漸化式ができます(※tは0以上の整数とする)。
仮にx(0)=0.1、a=3.2とするとx(1)=0.288となります。同様に計算するとx(2)=0.656…、x(3)=0.721…、x(4)=0.642…、x(5)=0.735…となり0.6と0.7ぐらいの値が交互に出てくるらしいとわかります。この計算を続けると最終的には二つの異なる値を交互にとる解に収束していくので、これを「周期2の解」と呼びます。出発点となるx(0)の値を0.1以外に変えても結果は同じです。
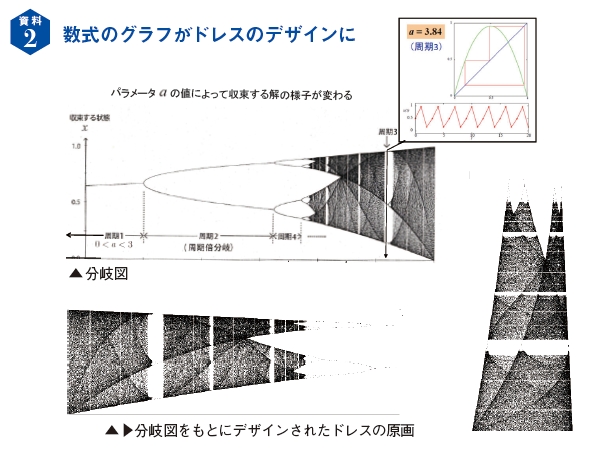
一方でパラメータaの値を変えると周期1、周期4、あるいは周期が無限大の状態=カオスになったりします。パラメータaの値によって収束する解が変わる。その様子を表すために描くのが分岐図です。この分岐図は大変美しいため、これを原画としてドレスをつくりファッションショーに出すと世界中で話題になりました(資料2)。
ちなみに先ほどの例で周期無限大のカオス状態の場合に、初期値を仮にx(0)=0.1 とx(0)=0.11とわずかでも異なる設定にするとどうなるか。二つの漸化式の解は指数関数で離れていきます。これをバタフライ効果と呼びます。「北京での小さなチョウの羽ばたきが、ニューヨークで嵐を起こす」といったたとえ話を使って説明される現象です。
資料2
次に病気を未然に防ぐプロジェクトを紹介します。といっても単純に健康状態を保とうというのではなく、病気になりそうだけどまだなっていない状態が対象です。要するにもうすぐ病気になりそうな状態を事前に察知し、発病する前に治してしまうのです。
では病気になる前の「未病」とは、いったいどんな状態でしょうか。健康状態から疾病状態に至る間には、時間の流れがあります。そのなかのどこかをピンポイントで「未病」と定義できれば、未病の詳しい研究ができます。
そこで注目したのが「臨界状態遷移」です。例えばきれいなサンゴ礁が、環境の悪化により破壊される場合を考えてみましょう。環境が徐々に悪化していく中で、ある段階を超えると元に戻せなくなります。いきなり破壊されるのではなく、状態が大きく変わる前には何らかの予兆信号が出ている。この信号を検出し、その段階で対応すれば大きな悪化を防げます。
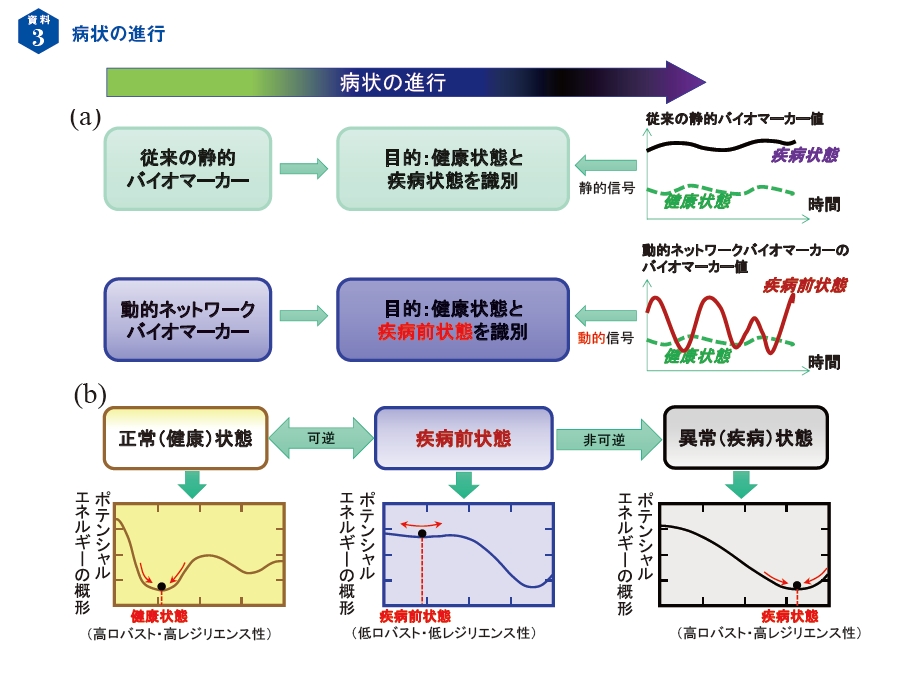
この考え方を病気に応用するには、予兆信号の検出がカギとなります。従来のバイオマーカーを使えば、一定値以上が病気で、別の一定値以下が健康と分けられます。これに対して、このような静的なものさしではなく、動的な揺らぎとして捉えるのが、動的ネットワークバイオマーカーの考え方です。
正常な状態とは安定した状態、資料3の図の凹の底にいるようなものです。これだと少々揺さぶられて底の位置からずれても、すぐに元の位置に戻ります。ところが発病前の状態になると、少し揺さぶられるだけで大きく揺らいでしまい、さらに揺らぎが大きくなると異常状態、つまり疾病状態へと落ちていきます。
正常な状態と未病状態の違いをどうやって見分けるのか。ポイントは揺らぎの大きさで、未病状態のほうが、同じ力で押された場合の揺らぎが大きくなる。この大きな揺らぎを検出するのが、「DNB」動的ネットワークバイオマーカーです(資料3)。
DNBにより、メタボリックシンドロームマウスの未病状態を検出し、そのマウスに漢方薬を与えた際に揺らぎが減少して症状が改善する効果が確かめられたりしています。アメリカでのインフルエンザに関するヒトのデータでも、未病状態すなわちもうすぐ発病する状態をDNBにより発病前に検出できることが明らかになっています。
動的ネットワークバイオマーカーの考え方は、病気以外にも応用できます。これを使えば、複雑なシステムが状態遷移を起こす前の予兆を検出可能になり、新型コロナの社会的流行の予兆を察知したり、経済データから経済の大きな変動の予兆を事前につかめたりします。このように一つの理論をさまざまな分野に応用できるのが、数学ならではの特徴です。
資料3
この数年で、深層学習やディープラーニングなどの用語が一般的にも広く知られるようになり、今ではAIの技術者がニューラルネットワークを積極的に使って研究しています。ところが30年前は、AIとニューラルネットワークは別々の研究分野だったのです。それが一緒になってきた背景には、両者のお手本となっている脳科学の進歩があります。
脳内のニューロンで起こっている電気パルスの動きは、コンピュータに似ています。ただしコンピュータと違って脳の活動電位はとても遅い。なのに高度な情報処理をしなければならないため、脳では並列分散処理が非常に発達しています。
それでいながら人の脳は、約1000億の神経細胞をわずか20Wの電力で動かしています。同じように1000億の神経細胞から構成される数理モデルを、スーパーコンピュータで動かそうとすると、途方もなく膨大な電力が必要です。だから脳と同じぐらい省電力で動き、しかも脳のように高度に発達した情報処理システムをつくるのが、現在研究者たちの大きな目標となっています。
AIの実力は囲碁や将棋で証明されています。けれどもペア碁で、人とAIを組ませたペアでは、人同士のペアよりも強いとは限りません。なぜなら今のAIには、人の心を読む力がないからです。とすれば、人とAI、つまり人間の知能と人工知能がうまく協調できれば、より強力で新たな知能が生まれるのではないか。これがNI(Neuro-Intelligence)、現在の私の重要研究テーマの一つです。

この世の中に実在するダイナミカルに変動する現象を一つ取り上げて、その現象を生み出すからくりを考えてください
夏休みが残り少なくなり課題に追われているので、勉強のやる気について考えてみました。やる気は確かに変動します。やる気を向上させるからくりには、精神的と生物的の二つがあると考えます。精神的なからくりは、勉強に対して楽しさを覚えたときに機能します。例えば記述問題で満点を取ったときや、志望校判定でA判定を取ったときなどです。生物的なからくりは、起床の3時間後に最も多く分泌されるアドレナリンと、空腹時に胃から出るグレリンが脳を刺激してやる気を起こしてくれます。方程式「精神的からくり×生物的からくり」をうまく機能させると、やる気と集中力が高まるはずです。

先生の講評
精神的と生物的の二つを取り上げたのは鋭い論点です。デカルトが唱えた「心身二元論」的思考を勉強のやる気に応用したとも考えられます。生物的なやる気部分は測定できるので、精神的なやる気部分の測定が、今後の脳科学の重要課題となります。さらにこの二つが単純な掛け算なのか、もっと複雑な関数として捉えるべきなのか。深く考えさせられるテーマだと思いました。