数学
全体概観
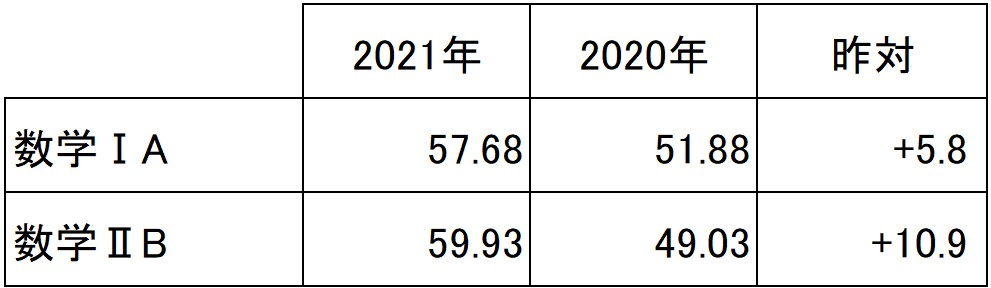
■大学入学共通テストでは数学平均点がⅠA・ⅡB 共に上昇
数学ⅠAの平均点は57.68点(昨年+5.8点)、数学ⅡBで59.93点(昨年+10.9点)となり平均点は問題の難易度が高まったのに対して昨年と比べて高まっている。 (また2013年以来、8年振りに数学ⅡBが数学ⅠAの平均点を上回った。)
全体概観
■大学入学共通テストでは数学平均点がⅠA・ⅡB 共に上昇
数学ⅠAの平均点は57.68点(昨年+5.8点)、数学ⅡBで59.93点(昨年+10.9点)となり平均点は問題の難易度が高まったのに対して昨年と比べて高まっている。 (また2013年以来、8年振りに数学ⅡBが数学ⅠAの平均点を上回った。)

数学② 数学ⅡB
全体概観
第1問〔2〕は会話文で指数関数と三角関数の類似性に関する問題が出題された。解答する問題のページ数は20年度の10~12ページから14~16ページと大幅に増加した。
| 大問数 |
減少
|
変化なし
|
増加
|
| 難易度 |
易化
|
やや易化
|
昨年並み
|
やや難化
|
難化
|
第1問[1]は三角関数を含む関数の最大・最小を合成から考察する問題、[2]は指数関数の特別な性質を、生徒の会話文を通じて考察する問題であった。
第2問は微分・積分の問題で、放物線や3次関数のグラフについて、その接線、それらが囲む部分の面積、最大・最小に関する問題である。
選択問題の第3問~第5問は、順に「確率分布と統計的な推測」「数列」「ベクトル」の分野で、試行調査の問題の順を踏襲している。第3問確率分布と統計的な推測の問題は、昨年までのセンター試験と同様に、正規分布表を利用して確率計算等を行う問題であった。第4問の数列の問題は、等差数列、等比数列、そして漸化式を絡めた問題になっている。第5問ベクトルの問題は、平面で正五角形、そして空間で正十二面体を扱う問題であった。
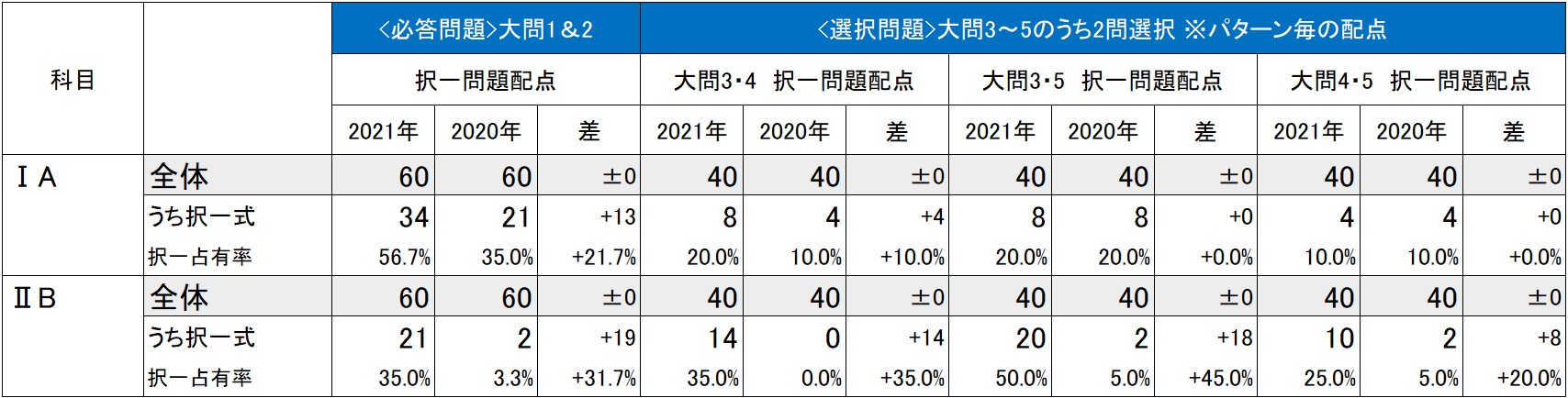
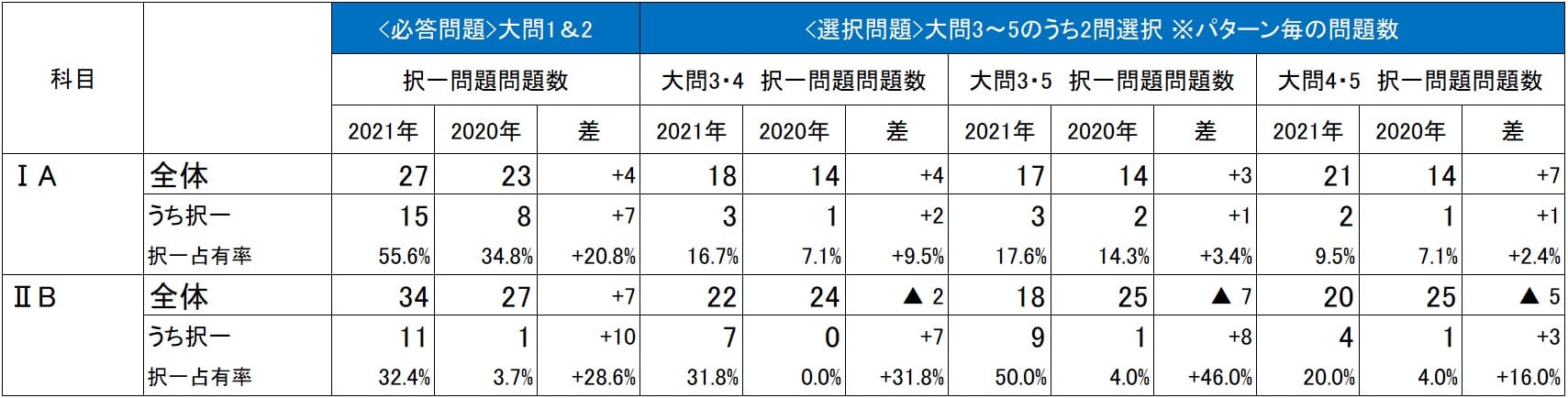
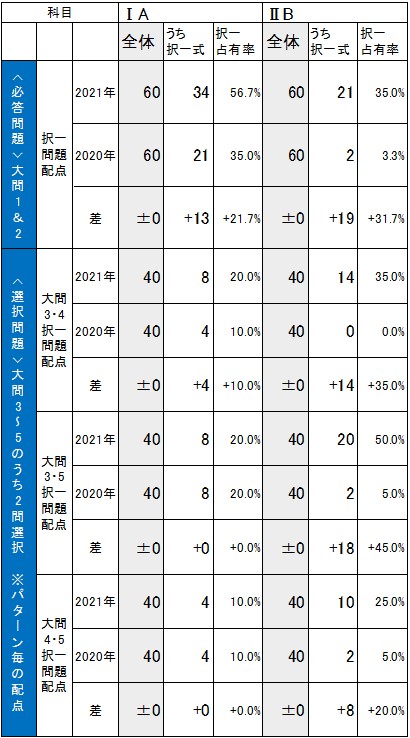
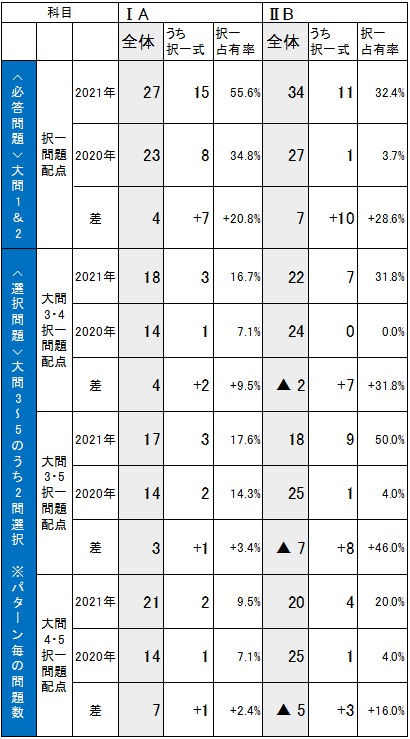
20年度センター試験よりも、与えられた選択肢から選ぶ形式の問題が増加している。解答する問題が20年度センター試験の10~12ページから14~16ページと大幅に増え、取り組みにくい設問も随所にあるが、全体的にやや易化した。
| 年度 | 大問 | 出題分野 | 配点 | |
| 2021 | 第1問 | [1] 三角関数 | 30 | |
| [2] 指数関数・対数関数 | ||||
| 第2問 | 微分法と積分法 | 30 | ||
| 第3問 | 2問選択 | 確率分布と統計的な推測 | 20 | |
| 第4問 | 数列 | 20 | ||
| 第5問 | ベクトル | 20 | ||
| 2020年以前はセンター試験 | ||||
| 年度 | 大問 | 出題分野 | 配点 | |
| 2020 | 第1問 | [1] 三角関数 | 30 | |
| [2] 指数関数・対数関数 | ||||
| 第2問 | 微分法と積分法 | 30 | ||
| 第3問 | 2問選択 | 数列 | 20 | |
| 第4問 | ベクトル | 20 | ||
| 第5問 | 確率分布と統計的な推測 | 20 | ||
| 2019 | 第1問 | [1] 三角関数 | 30 | |
| [2] 指数関数・対数関数 | ||||
| 第2問 | 微分法と積分法 | 30 | ||
| 第3問 | 2問選択 | 数列 | 20 | |
| 第4問 | ベクトル | 20 | ||
| 第5問 | 確率分布と統計的な推測 | 20 | ||
| 2018 | 第1問 | [1] 三角関数 | 30 | |
| [2] 指数関数・対数関数 | ||||
| 第2問 | [1] 微分法と積分法 | 30 | ||
| [2] 微分法と積分法 | ||||
| 第3問 | 2問選択 | 数列 | 20 | |
| 第4問 | ベクトル | 20 | ||
| 第5問 | 確率分布と統計的な推測 | 20 | ||
| 2017 | 第1問 | [1] 三角関数 | 30 | |
| [2] 指数関数・対数関数 | ||||
| 第2問 | 微分法と積分法 | 30 | ||
| 第3問 | 2問選択 | 数列 | 20 | |
| 第4問 | ベクトル | 20 | ||
| 第5問 | 確率分布と統計的な推測 | 20 | ||
【参考】過去の平均点の推移
| 2020 | 2019 | 2018 | 2017 | 2016 | 2015 |
|---|---|---|---|---|---|
| 49.03 | 53.21 | 51.07 | 52.07 | 47.92 | 39.31 |
 大学受験(大学入試)対策の塾・予備校なら東進
大学受験(大学入試)対策の塾・予備校なら東進


 大学受験(大学入試)対策の塾・予備校なら東進
大学受験(大学入試)対策の塾・予備校なら東進